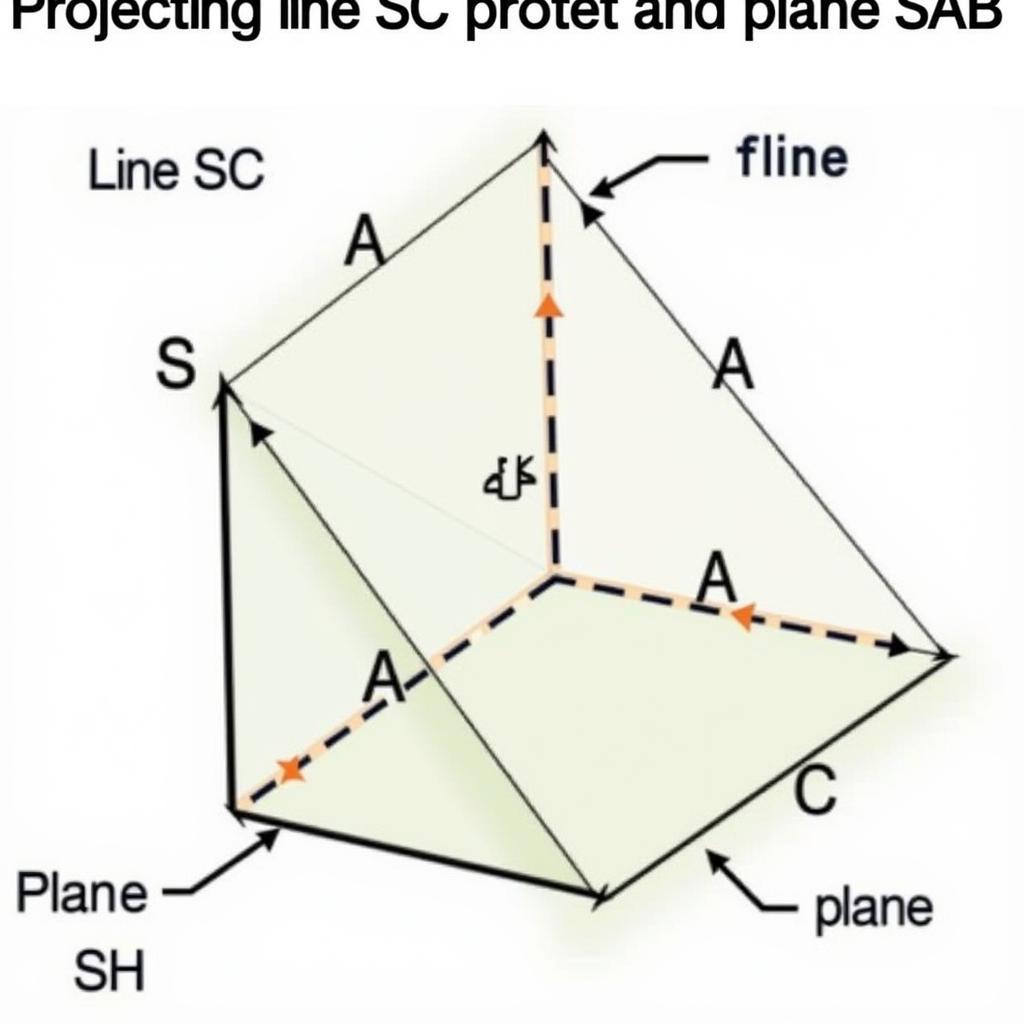
Tính Góc Giữa Sc Và Sab là một bài toán hình học không gian quen thuộc, thường xuất hiện trong chương trình toán lớp 11 và 12. Việc nắm vững cách tính góc này không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn rèn luyện tư duy hình học không gian, một kỹ năng quan trọng trong việc học tập và nghiên cứu các lĩnh vực khoa học kỹ thuật.
Phương Pháp Xác Định Góc Giữa Đường Thẳng và Mặt Phẳng
Để tính góc giữa SC và SAB, trước hết ta cần hiểu cách xác định góc giữa một đường thẳng và một mặt phẳng. Góc giữa đường thẳng d và mặt phẳng (P) được định nghĩa là góc giữa đường thẳng d và hình chiếu d’ của nó lên mặt phẳng (P). Lưu ý rằng góc này luôn là góc nhọn hoặc bằng 0. Trong trường hợp đường thẳng d vuông góc với mặt phẳng (P), góc giữa chúng bằng 0.
Các Bước Tính Góc Giữa SC và SAB
Để tính góc giữa SC và SAB, ta thực hiện các bước sau:
- Xác định hình chiếu của SC lên mặt phẳng (SAB): Đây là bước quan trọng nhất. Thông thường, ta tìm điểm H là hình chiếu của C lên (SAB). Khi đó, SH là hình chiếu của SC lên (SAB).
- Tính góc giữa SC và SH: Góc cần tìm chính là góc CSH. Ta có thể sử dụng các công thức lượng giác trong tam giác vuông SCH để tính góc này.
- Kết luận: Góc giữa SC và SAB chính là góc CSH.
Hình chiếu của SC lên SAB
Ví Dụ Minh Họa Tính Góc
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = a. Tính góc giữa SC và (SAB).
- Xác định hình chiếu: Vì SA vuông góc với (ABCD) nên SA vuông góc với AB. Do đó, AB vuông góc với (SAD), suy ra AB vuông góc với AD. Kẻ AH vuông góc với SB, ta có AH vuông góc với (SBC), suy ra AH vuông góc với SC. Mặt khác, AC vuông góc với BD (do ABCD là hình vuông). Suy ra BD vuông góc với (SAC). Kẻ CI vuông góc với SA, ta có CI vuông góc với (SAB), do đó CH là hình chiếu vuông góc của SC lên (SAB).
- Tính góc: Trong tam giác vuông SAC, ta có: 1/SC² = 1/SA² + 1/AC² = 1/a² + 1/(2a²) = 3/(2a²). Vậy SC = a√(2/3). Trong tam giác vuông SCH, ta có sin(SCH) = CH/SC. Tính được CH = a√6/3. Suy ra sin(SCH) = (a√6/3)/(a√(2/3)) = 1/√2. Vậy góc SCH = 45 độ.
- Kết luận: Góc giữa SC và (SAB) là 45 độ.
Ví dụ tính góc giữa SC và SAB
Một Số Lưu Ý Khi Tính Góc Giữa SC và SAB
- Cần xác định chính xác hình chiếu của SC lên mặt phẳng (SAB). Sai lầm trong bước này sẽ dẫn đến kết quả sai.
- Có thể sử dụng nhiều phương pháp khác nhau để xác định hình chiếu, tùy thuộc vào dữ kiện bài toán.
- Nên vẽ hình cẩn thận để hình dung rõ ràng bài toán.
Ông Nguyễn Văn A, giáo viên Toán tại trường THPT Chuyên Hà Nội – Amsterdam, chia sẻ: “Việc thành thạo tính góc giữa đường thẳng và mặt phẳng là nền tảng quan trọng để giải quyết các bài toán hình học không gian phức tạp hơn. Học sinh cần nắm vững các kiến thức cơ bản và luyện tập thường xuyên để nâng cao kỹ năng.”
Bà Trần Thị B, giảng viên Đại học Sư Phạm Hà Nội, bổ sung: “Ngoài việc áp dụng công thức, học sinh cần rèn luyện tư duy hình học không gian, khả năng phân tích và tổng hợp thông tin để giải quyết bài toán một cách hiệu quả.”
Lưu ý khi tính góc giữa SC và SAB
Kết luận
Tính góc giữa SC và SAB là một dạng bài toán quan trọng trong hình học không gian. Bằng việc nắm vững phương pháp và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài toán liên quan. Hiểu rõ cách tính góc này sẽ giúp bạn xây dựng nền tảng vững chắc cho việc học tập và nghiên cứu các lĩnh vực khoa học kỹ thuật sau này.
FAQ
- Góc giữa đường thẳng và mặt phẳng có thể là góc tù không? (Không, góc này luôn nhọn hoặc bằng 0).
- Làm thế nào để xác định hình chiếu của đường thẳng lên mặt phẳng? (Tìm hình chiếu của hai điểm bất kỳ trên đường thẳng lên mặt phẳng, sau đó nối hai hình chiếu đó lại).
- Khi nào góc giữa đường thẳng và mặt phẳng bằng 0? (Khi đường thẳng song song hoặc nằm trong mặt phẳng).
- Công thức nào thường được sử dụng để tính góc giữa đường thẳng và mặt phẳng? (Công thức lượng giác trong tam giác vuông).
- Có những phương pháp nào để tính góc giữa đường thẳng và mặt phẳng? (Phương pháp hình chiếu, phương pháp vector).
- Tại sao cần nắm vững cách tính góc giữa đường thẳng và mặt phẳng? (Đây là kiến thức cơ bản và quan trọng trong hình học không gian).
- Làm thế nào để luyện tập hiệu quả cách tính góc giữa đường thẳng và mặt phẳng? (Giải nhiều bài tập đa dạng và xem lại các bài giảng).
Bạn có thể tham khảo thêm các bài viết khác trên website BÓNG ĐÁ GOXPLORE về các chủ đề liên quan đến hình học không gian.
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 0372999996, Email: [email protected] Hoặc đến địa chỉ: 236 Cầu Giấy, Hà Nội. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
